Europäischer Abakus

Im europäischen Raum

herrscht heute beim Abakus traditionell eine klassische Ausführung vor. Die Rechenperlen sind waagerecht angeordnet, meist zu 10 untereinander liegenden Zeilen á zehn Perlen. Sie werden zum Rechnen somit waagerecht verschoben. Teils sind die Rechenperlen einer Zeile in nur einer Farbe, teils gebündelt je zu fünfen in einer Farbe. Leider ist in unserem Kulturkreis das Rechnen mit dem Abakus ins Kinderzimmer, als Spiel verdrängt und als Spielkram abgetan worden. Zum Erlernen von Rechenfertigkeiten wird er in der Grundschule aber wieder zusehends genutzt. Der Abakus ist hier im Mathematikunterricht ein Medium unter vielen, das es geschickt von der Lehrkraft einzusetzen gilt. In anderen Kulturkreisen, insbesondere im asiatischen Bereich, erlernen die Kinder in der Grundschule das Rechnen mit dem Abakus. Vielleicht sind sie ja auch deshalb unseren Grundschulkindern in der Rechenfertigkeit in aller Regel deutlich überlegen.

Zu den mathematischen Möglichkeiten von 10 Perlen auf einer Zeile hier noch ein paar Überlegungen. Da wir üblicherweise im Dezimalsystem, auch 10er-Zahlsystem, rechnen, benötigt man eigentlich nur 9 Perlen pro Zeile. 10 Perlen ist wohl traditionell zu sehen. Es ist eine Konzession an die Zahlvorstellung sowie das Erlernen von Rechenoperationen der Schülerinnen und Schüler der Grundschule, die mit einem Abakus das Rechnen einfacher internalisieren können. Sie können den Abakus augenscheinlich nutzen, um von Null bis 100 zu rechnen. Jeder Perle hat hier den Wert 1. Ob man von unten nach oben, oder oben nach unten rechnet, ist völlig egal. Die Kinder können sich letztlich auch eigene Verschiebemethoden ausdenken. Sinn macht es, wenn man auf Dauer die Nullstellung eindeutig festlegt, z.B. links.

	Abakus in Ausgangsstellung, also mit Darstellung der Zahl Null
	Abakus mit Darstellung der Zahl 44
	Abakus mit Darstellung der Zahl Hundert

Denkt man jedoch an ein Rechnen in einem 10er-Stellenwertsystem, dann ergeben sich noch ganz andere Möglichkeiten den Abakus mathematisch zu nutzen. Jetzt bekäme die unterste Zeile den Stellenwert 10 hoch Null (10⁰ = 1), die zweite Zeile den Stellenwert 10 hoch 1 (10¹ = 10), die dritte Zeile den Stellenwert 10 hoch 2 (10² = 100), u.s.w.. Die zehnte, oberste Zeile hätte dann den Stellenwert 10 hoch 9 (10⁹ = 1.000.000.000). Anders ausgedrückt, auf der unteren Zeile werden die Einer dargestellt, darüber die Zehner, dann die Hunderter, Tausender, Zehntausender u.s.w.. Somit wäre ein einfaches Rechen bis maximal 10¹⁰ - 1 = 10.000.000.000 - 1 = 9.999.999.999 machbar. Anders ausgedrückt, könnten wir jetzt leicht bis 10 Milliarden minus 1 rechnen. Für diese Rechnungen langt es aber mathematisch völlig, wenn 9 Perlen auf einer Zeile wären.

Für die bessere Verständlichkeit einer Stellenwertschreibweise sollte man die Perlen auf dem Abakus, so es die Bauart zulässt, senkrecht verschieben. Dann hat die rechte Perlenspalte den Wert k ^. 10⁰( k = 1, 2, 3, 4, 5, 6, 7, 8, 9), die zweite Perlenspalte von rechts den Wert k ^. 10¹( k = 1, 2, 3, 4, 5, 6, 7, 8, 9), ..., die linke Perlenspalte den Wert k ^. 10⁹( k = 1, 2, 3, 4, 5, 6, 7, 8, 9). Wir vereinbaren, dass wir von unten nach oben, in Anlehnung an einen chinesischen Abakus, rechnen. Immer noch bleibt so die maximal darzustellende Zahl die 9.999.999.999 = 10¹⁰ - 1 = 10.000.000.000 - 1. Bis hierhin kann man mit einfachen Algorithmen und Verschiebung der Perlen Rechnungen vornehmen.

	Abakus in Ausgangsstellung für eine Stellenwertdarstellung, also hier mit Darstellung der Zahl Null
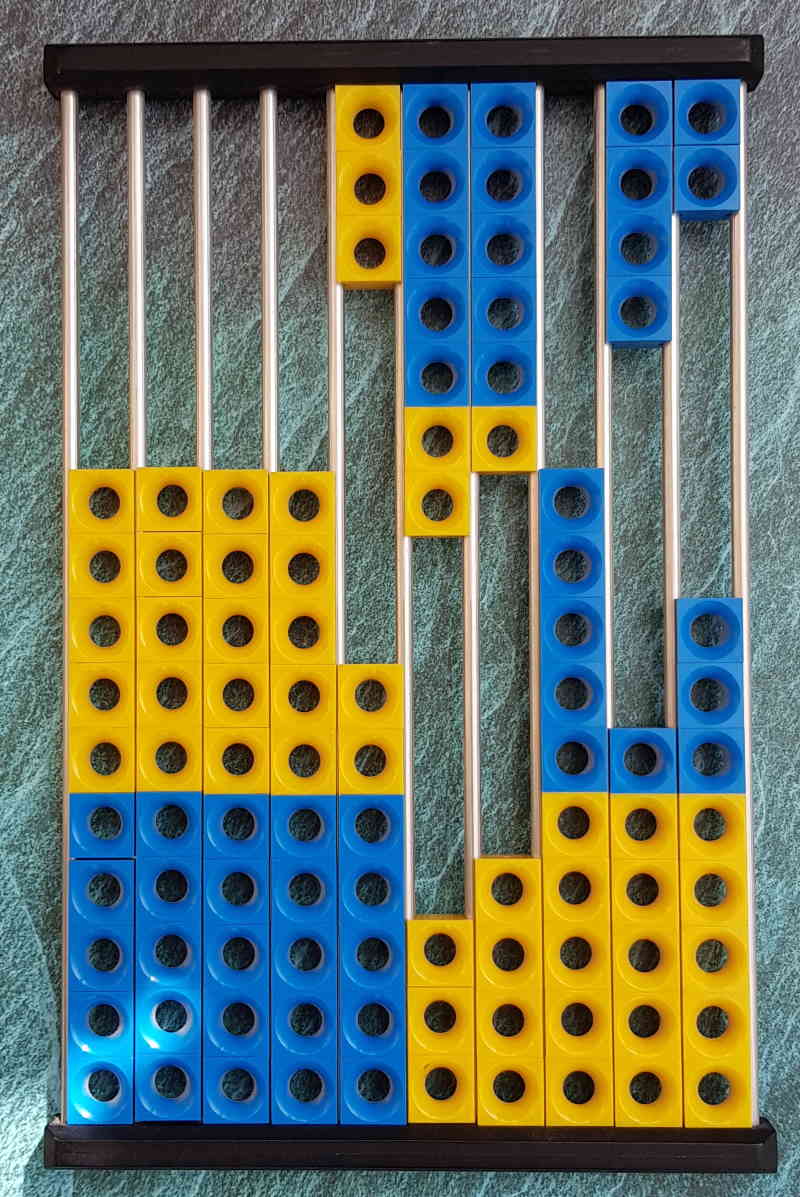	Darstellung der Zahl 376.042
	Darstellung der Zahl 9.999.999.999 = 10¹⁰ - 1 = 10.000.000.000 - 1

Es stellt sich die Frage, was passiert, wenn man 9.999.999.999 + 1 rechnet? Auch das ist mit etwas Überlegung logisch darstellbar.

Rechenschritt 1: Die rechte untere Perle muss nach oben verschoben (addiert) werden.

Rechenschritt 2: Alle Perlen der rechte Perlenspalte müssen nach unten verschoben und eine Perle zur nächsten Perlenspalte übertragen werden.

Darstellung der Zahl 10.000.000.000

Darstellung der Zahl 10.000.000.000 = 10¹⁰

Das Ganze kann man gedanklich mathematisch weiter auf die Spitze treiben. Wir haben pro Perlenspalte 10 Perlen, nutzen aber nur 9. Welche Zahl wird dargestellt, wenn man alle 10 Perlen nach oben geschoben hat? Nun, es ist die 10.111.111.111. Das ist die wirklich maximal darstellbare Zahl in einem dezimalen Stellenwertsystem auf einem europäischen Abakus. Aber Achtung, ab hier ist keine Addition mehr möglich. Außerdem muss man schon sehr genau überlegen, wie die Perlen bei z.B. einer Subtraktion verschoben werden.

Darstellung der Zahl 10.111.111.111

Darstellung der Zahl 10.111.111.111

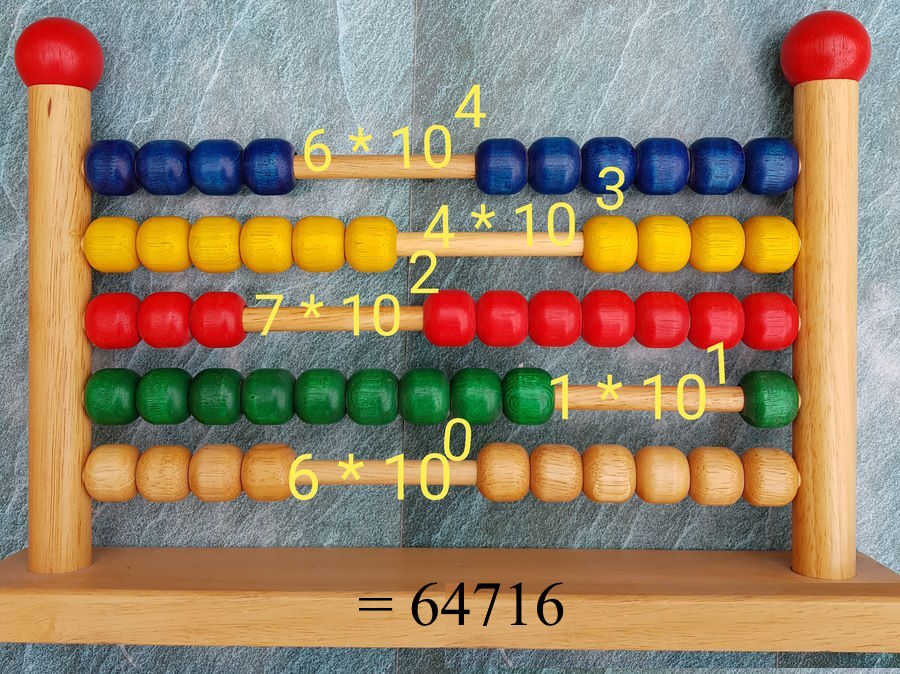
Bei einem europäischen Abakus gibt auch die grundsätzliche Möglichkeit in einem 11er-Stellenwertsystem zu rechnen. Das ergibt sich daraus, dass genau 10 Perlen auf einer Zeile angeordnet sind. Folglich ordnen wir, in Anlehnung an das Hexadezimalsystem (Stellenwertsystem auf der Basis 16), der Dezimalzahl "10" in einem 11er-Stellenwertsystem das "A" zu, also 10₁₀ = A₁₁. Wir nutzen den Abakus stellenwertgerecht wieder sinnvoller indem wir die Perlen senkrecht verschieben. Jetzt bekommt die rechte Spalte den Stellenwert 11 hoch Null (11⁰ = 1), die zweite Spalte von rechtes den Stellenwert 11 hoch 1 (11¹ = 11), die dritte Spalte von rechts den Stellenwert 11 hoch 2 (11² = 121), u.s.w.. Die zehnte, linke Spalte hat dann den Stellenwert 11 hoch 9 (11⁹ = 2.357.947.691). Somit ist ein Rechen bis maximal 11¹⁰ - 1 = 25,9374246 ^. 10⁹ - 1 machbar. Anders gesagt, können wir jetzt bis fast 26 Milliarden, ausgedrückt im Dezimalsystem, rechnen. Das ist zugegeben ein reines mathematisches Gedankenspiel ohne wirklich praktischen Nutzen. Meines Wissens rechnet keiner in einem 11er-Stellenwertsystem und es gibt auch keine sinnvolle Anwendung hierfür. Anders bei einem Hexadezimalsystem, das eine Anwendung im Bereich der IT-Technik findet.

Angenommen wir hätten die Zahl 614A3₁₁ in einem 11er-Stellenwertsystem. Welcher Zahl entspricht das in einem Dezimalsystem?

	614A3₁₁
=	6 ^. 11⁴+ 1 ^. 11³+ 4 ^. 11²+ A ^. 11¹+ 3 ^. 11⁰
=	6 ^. 11⁴+ 1 ^. 11³+ 4 ^. 11²+ 10 ^. 11¹+ 3 ^. 11⁰
=	6 ^. 14641+ 1 ^. 1331+ 4 ^. 121+ 10 ^. 11+ 3 ^. 1
=	87846 + 1331 + 484 + 110 + 3
=	89774₁₀