Der Abakus - eine alte
Rechenmaschine
Der Abakus
der Maya (Informatives)
Zum Aufbau des maya Abakus
Der Abakus der Maya, der
Nepohualtzintzin, ist nicht dafür gebaut, um damit in einem
10er-Zahlsystem (Dezimalsystem) zu rechnen. Das geht, dafür ist er aber nicht
sinnvoll gebaut. Die Rechenperlen sind in senkrechten Reihen angeordnet.
Sie
haben am oberen bzw. unteren Rahmen liegend ihre
Ausgangsstellung. Oben sind drei und unten vier Perlen. Das reicht mathematisch
optimal, um geschickt und schnell in einem 20er-Zahlsystem rechnen zu können.
Das war genau das Zahlsystem der Maya.
|
 |
|
| im Hintergrund der Abakus der Maya (Nepohualtzintzin) |
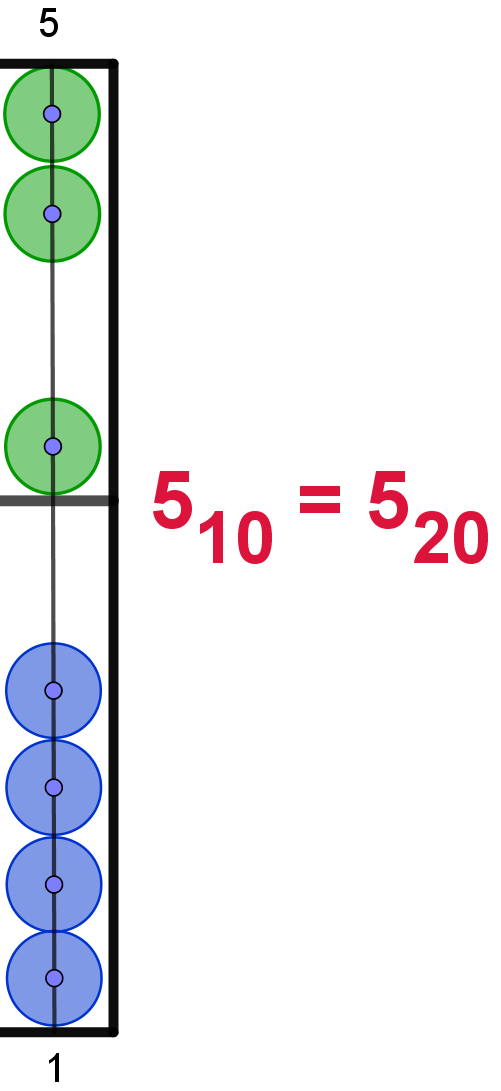
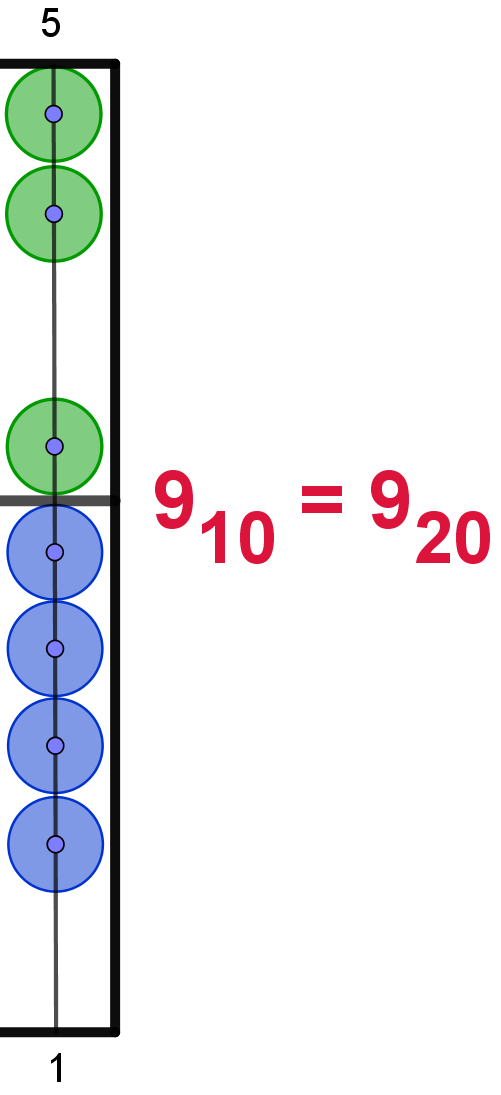
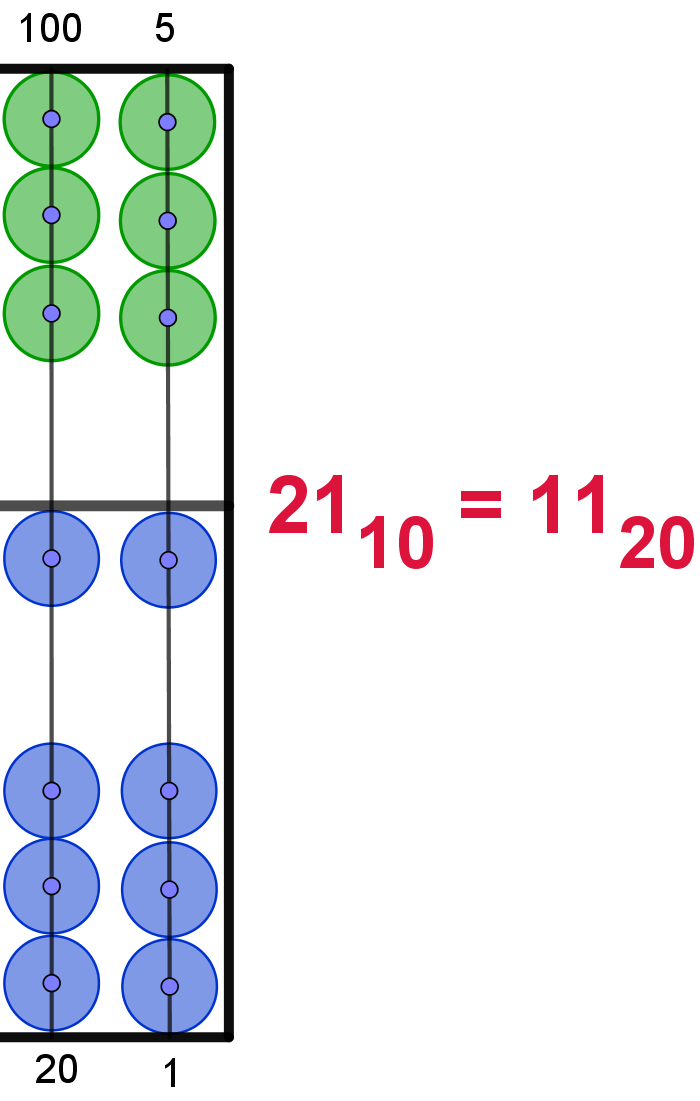
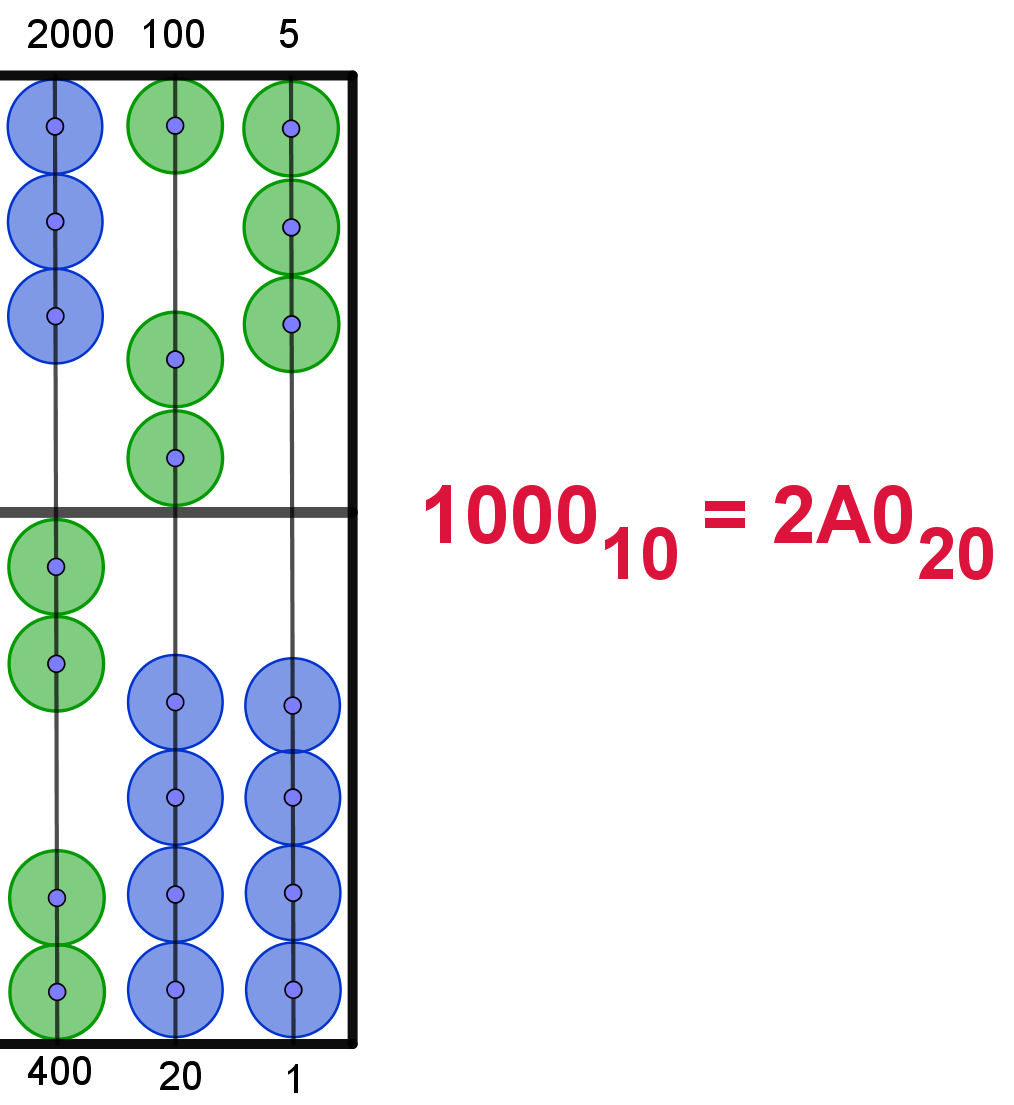
Die Zahlwerte der Perlen sind im Dezimalsystem
dargestellt. Hier ergibt sich als Einstellung 15610 =
7G20 |
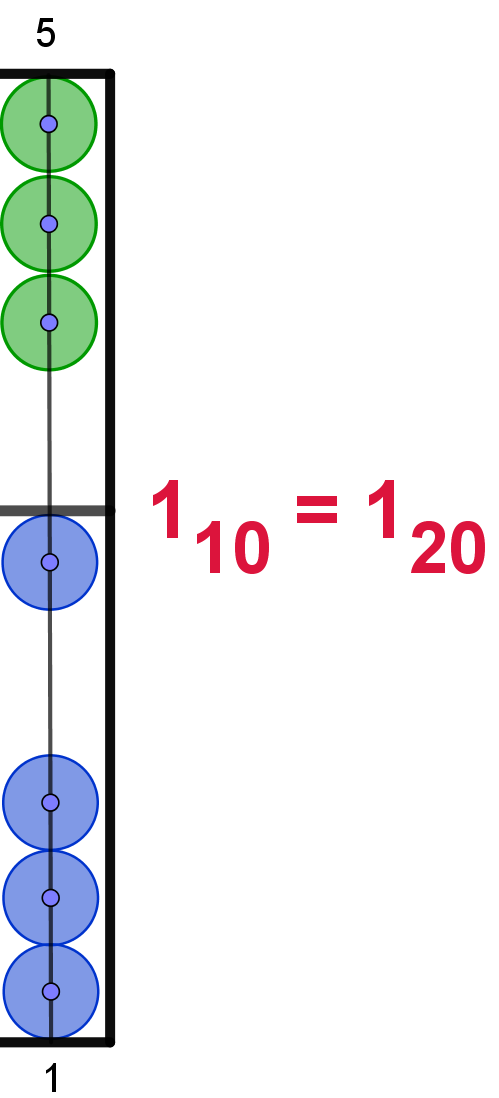
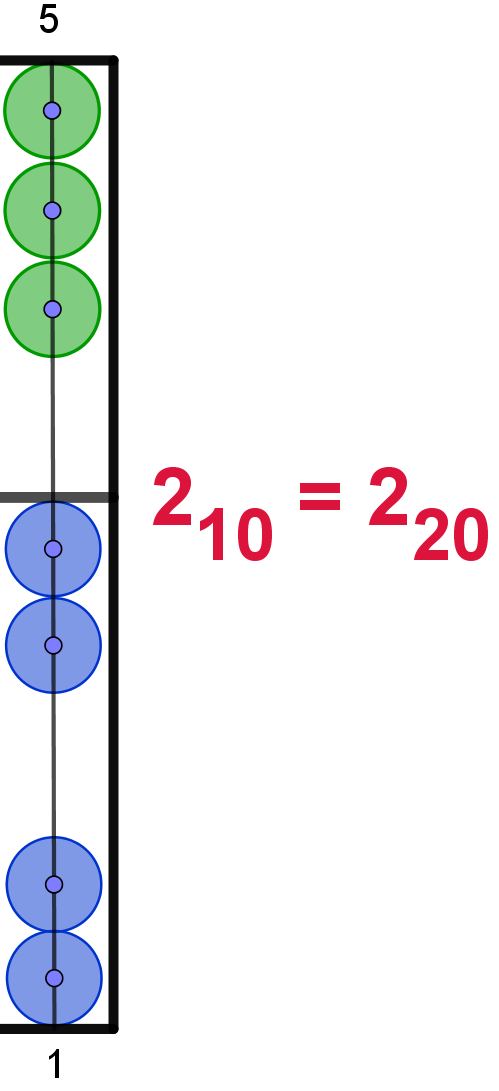
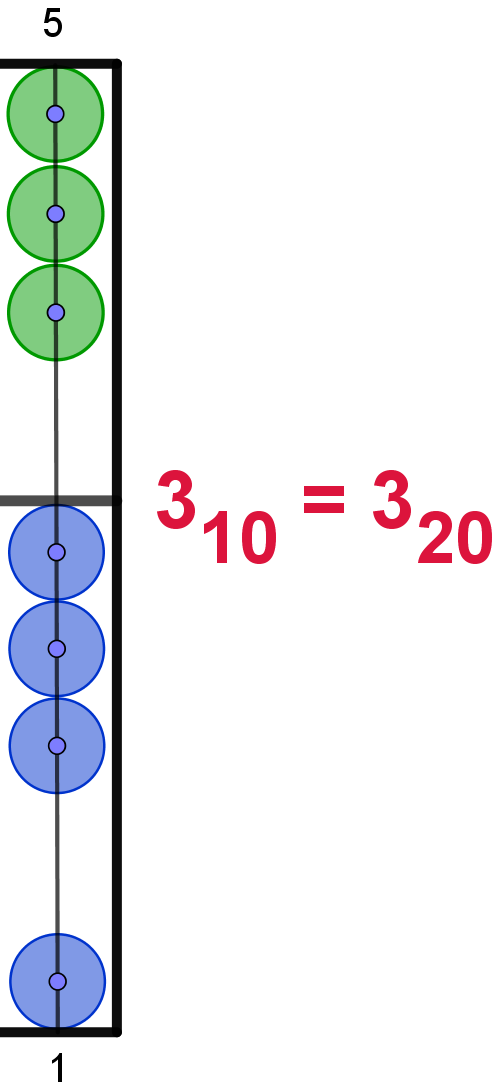
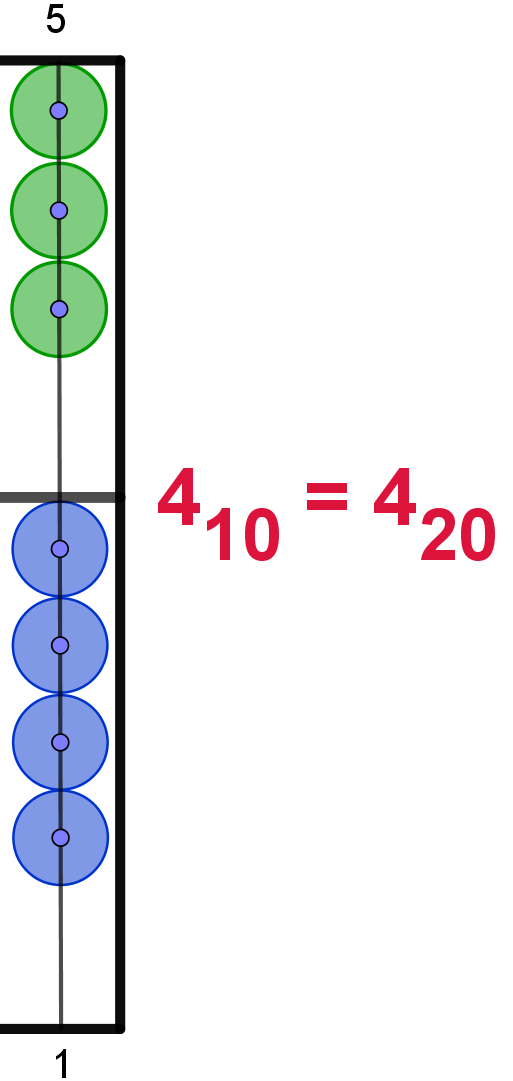
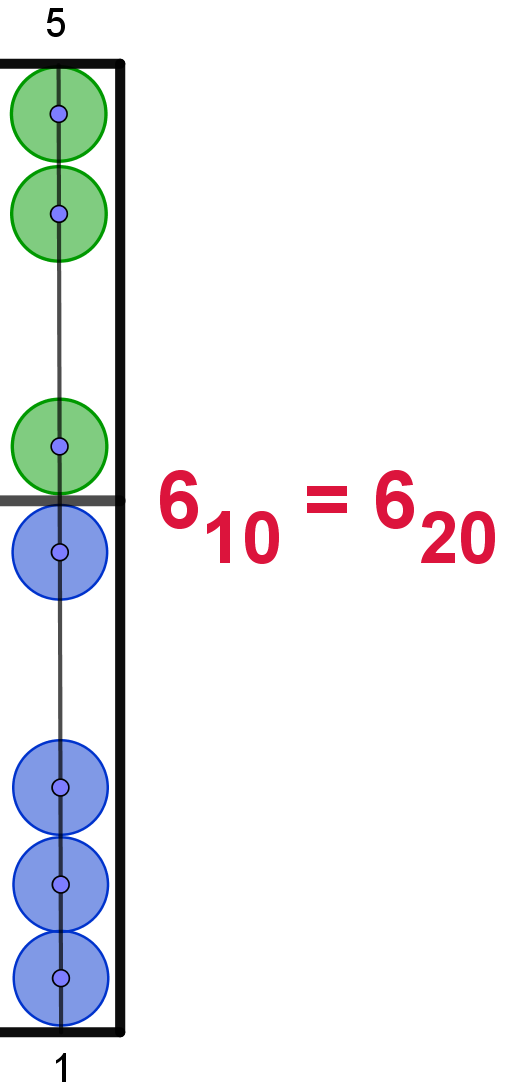
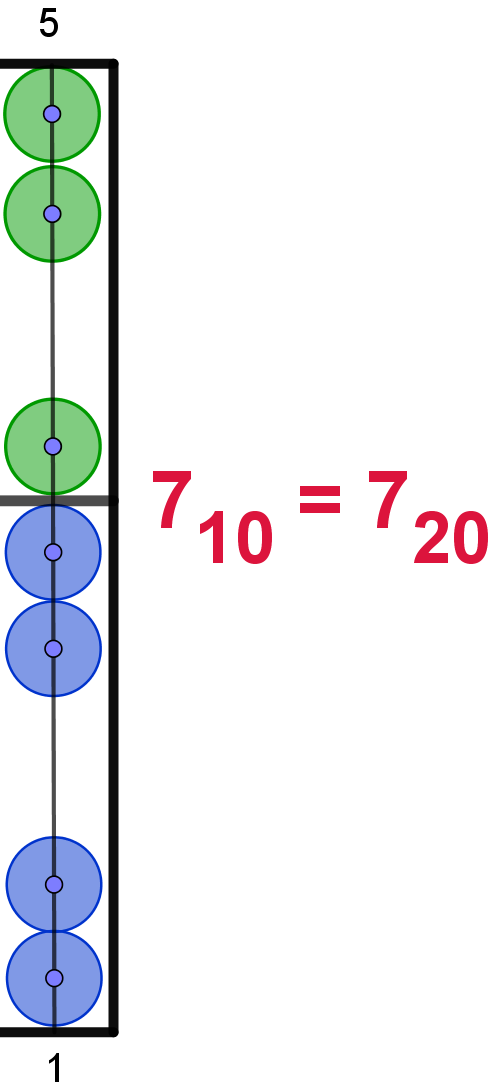
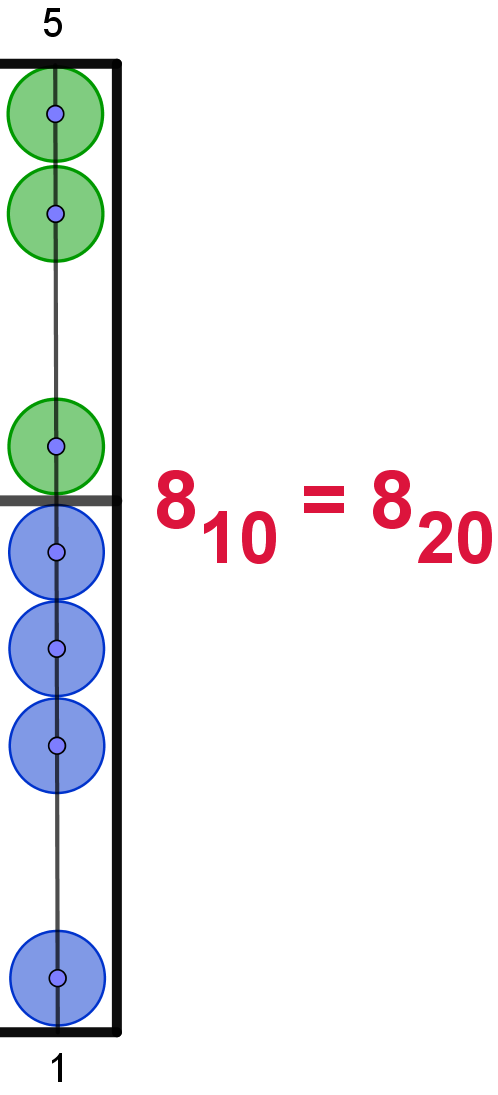
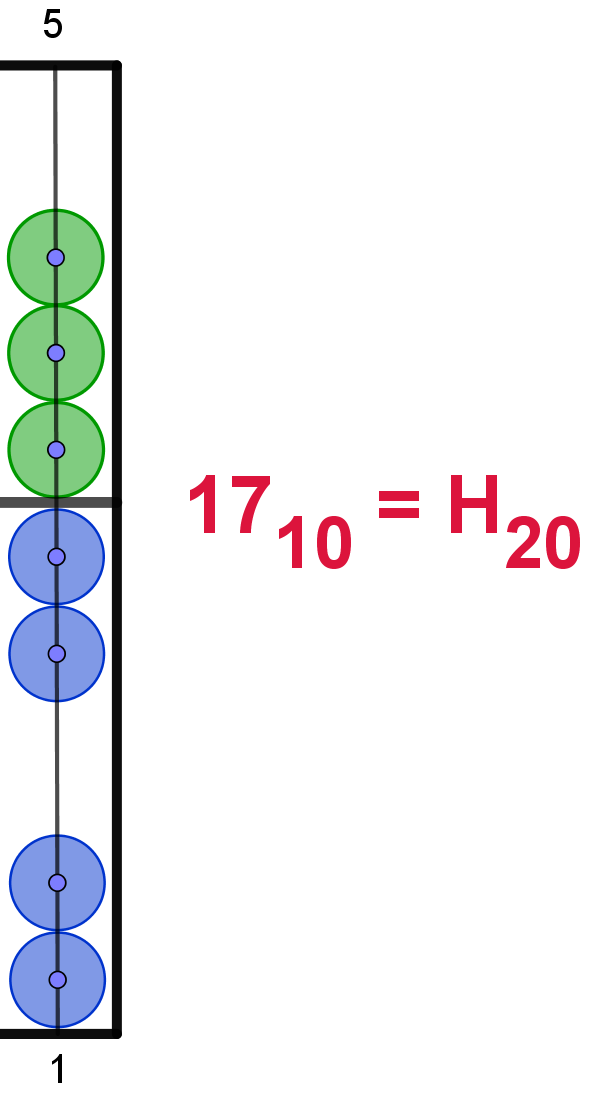
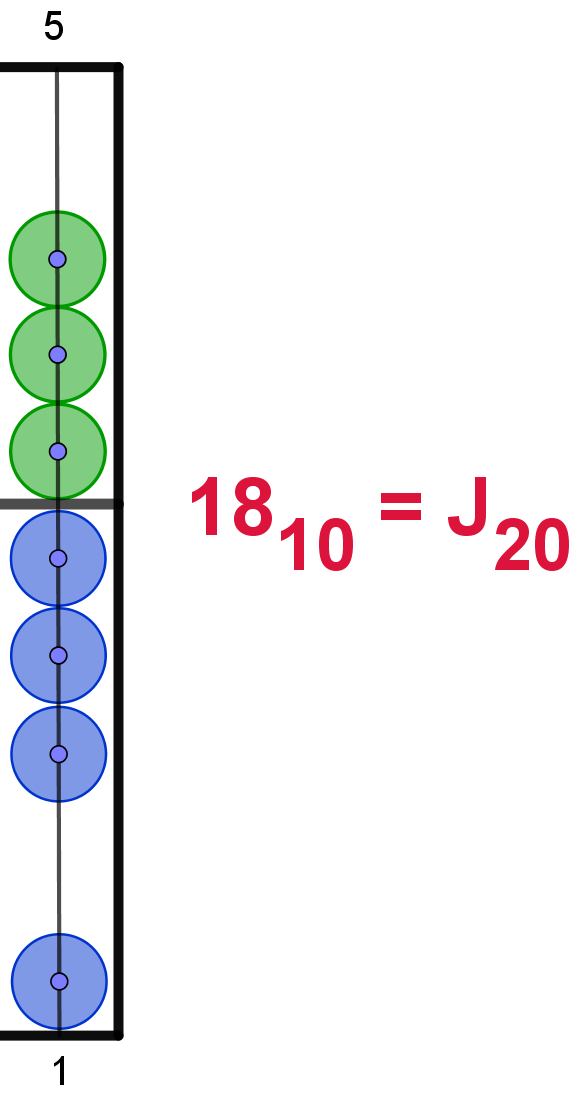
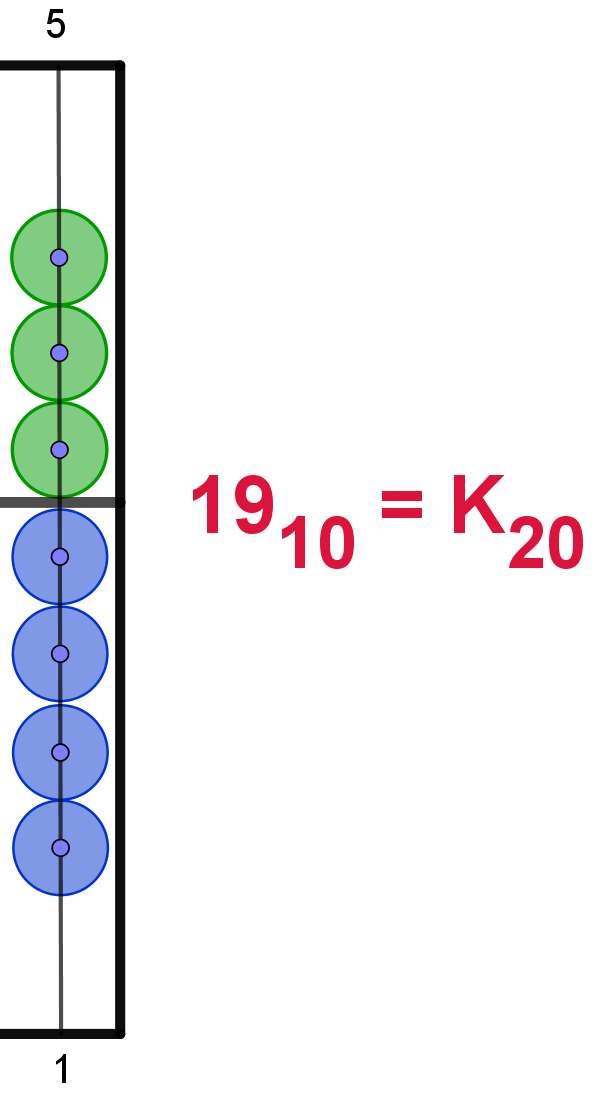
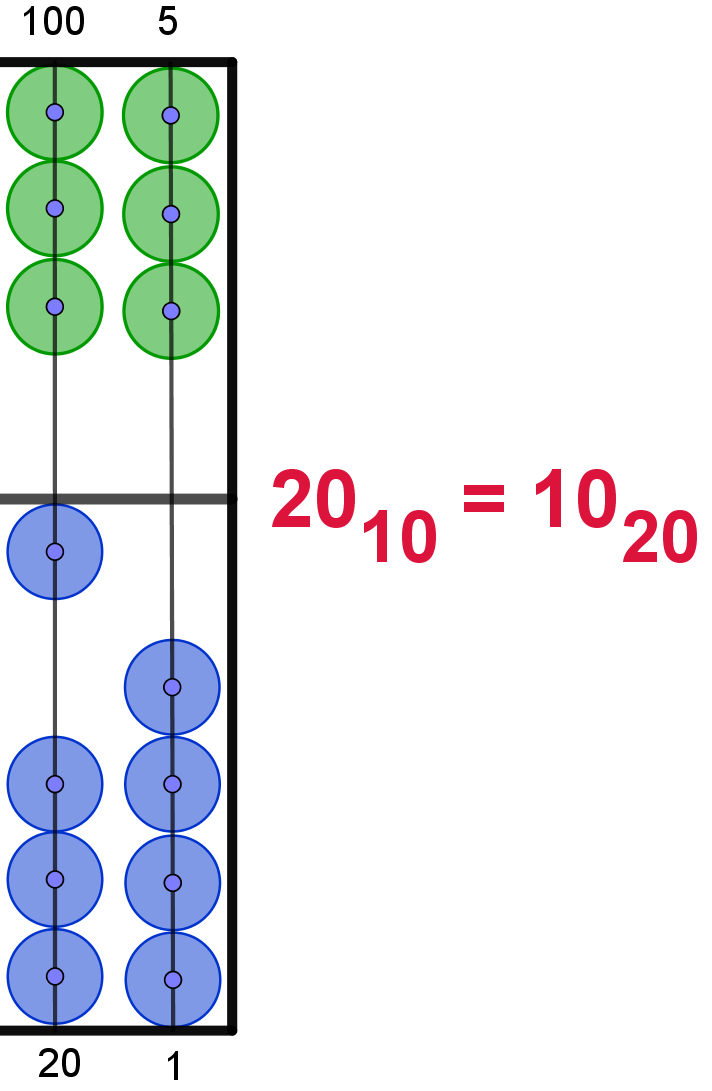
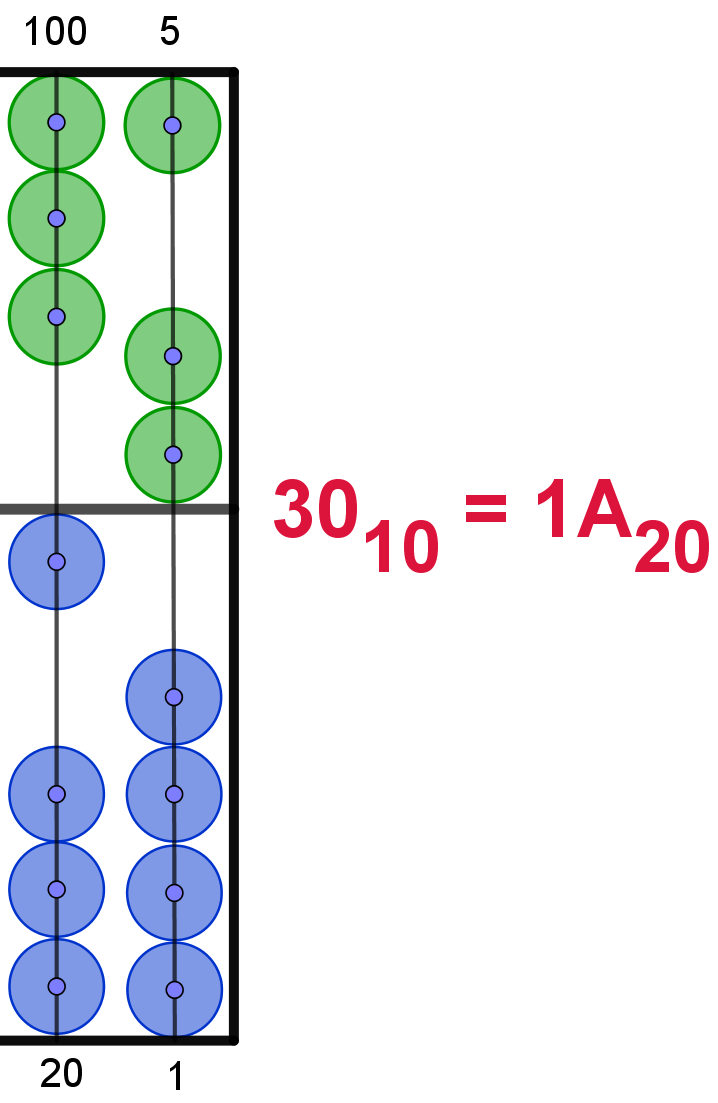
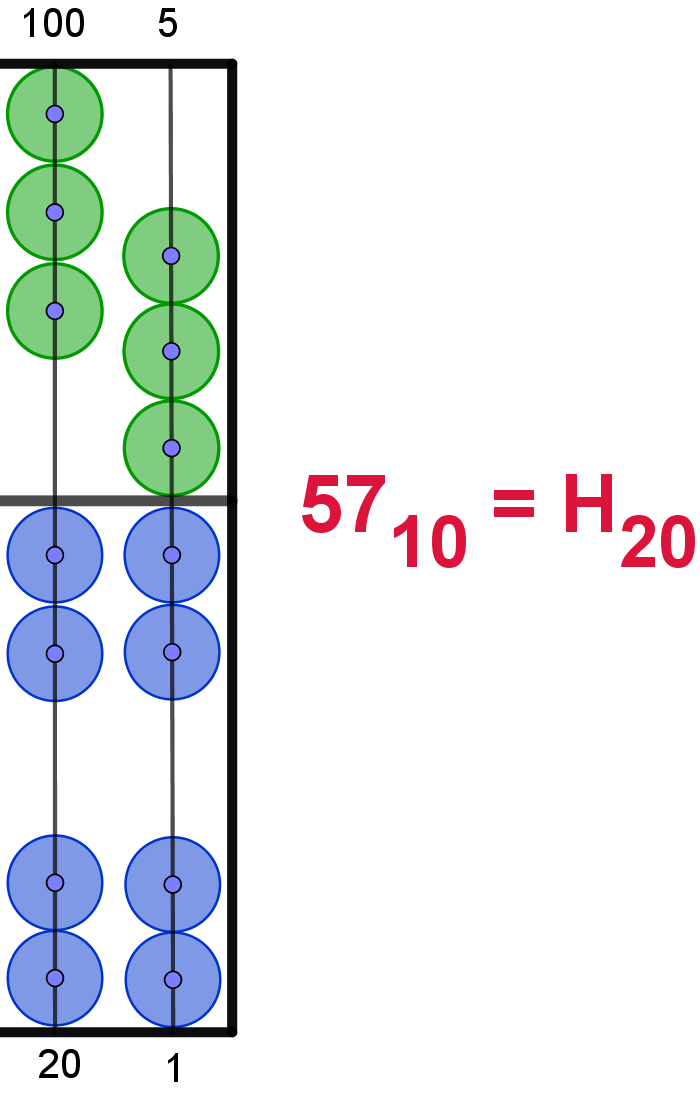
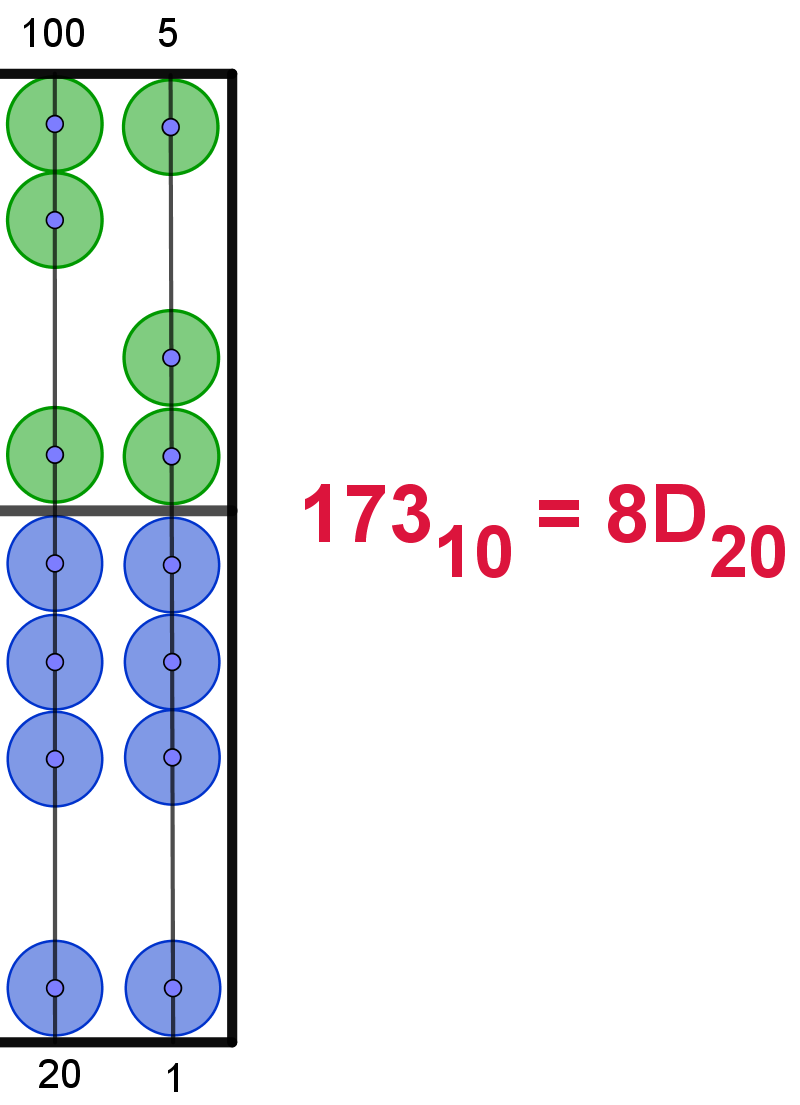
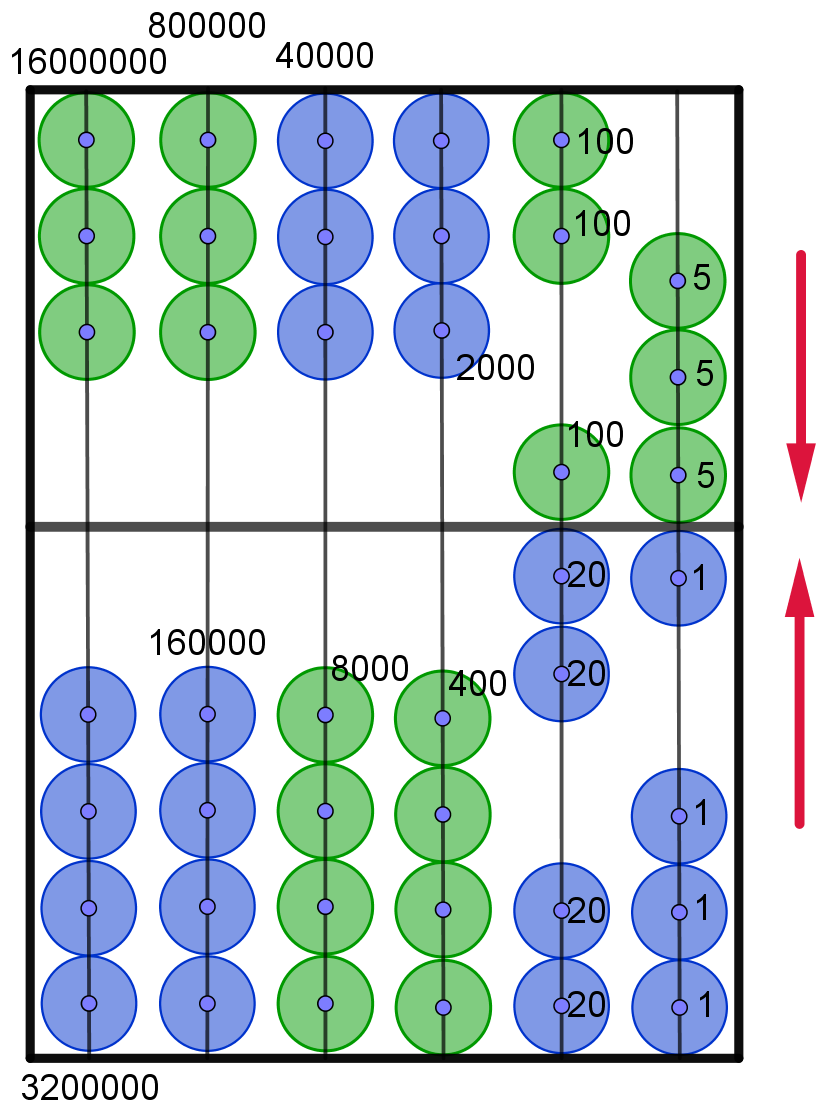
Hier die Darstellung der Zahlen von 110 bis 2010
im 20er-Zahlsystem. In Anlehnung an das Hexadezimalsystem werden die Ziffern
ab 1010 mit den Buchstaben von "A" bis "L" dargestellt. Um
Verwechselungen zu vermeiden, wird der Buchstabe "I" übersprungen. Die Maya
verwendeten hier bildliche Darstellungen.
|
Zahlsystem |
|
10er |
20er |
|
0 |
0 |
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
4 |
|
5 |
5 |
|
6 |
6 |
|
7 |
7 |
|
8 |
8 |
|
9 |
9 |
|
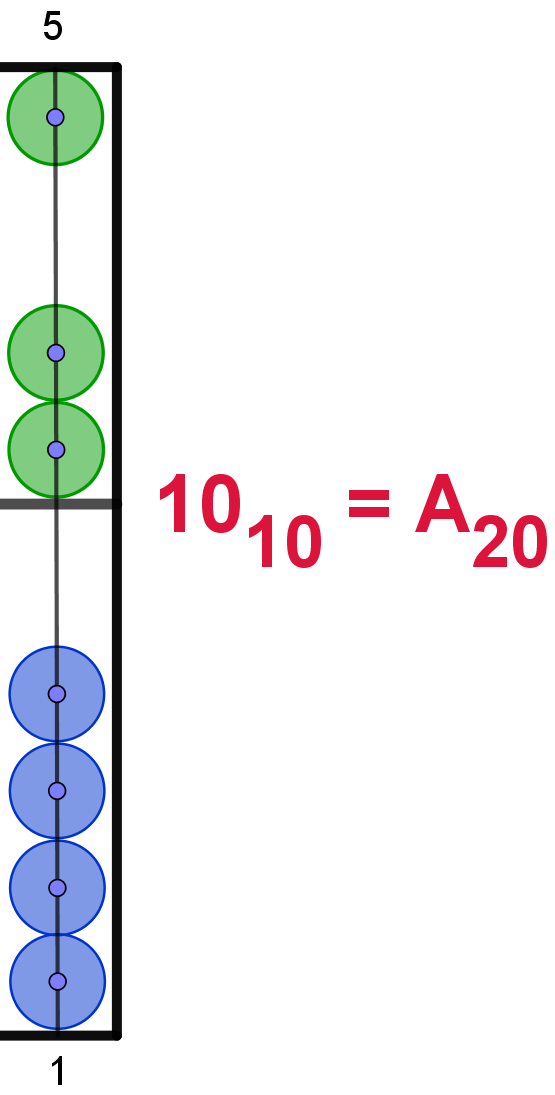
10 |
A |
|
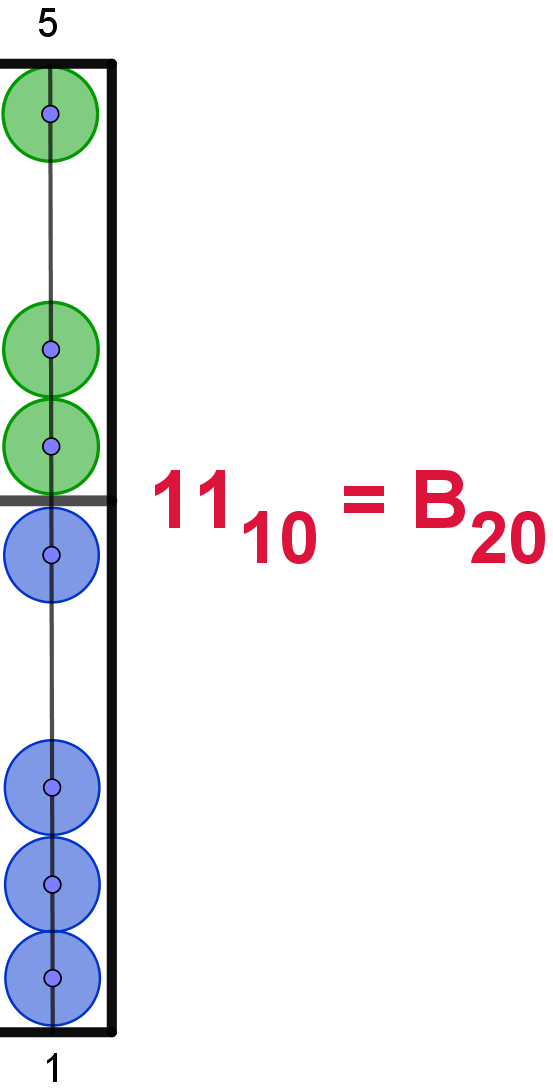
11 |
B |
|
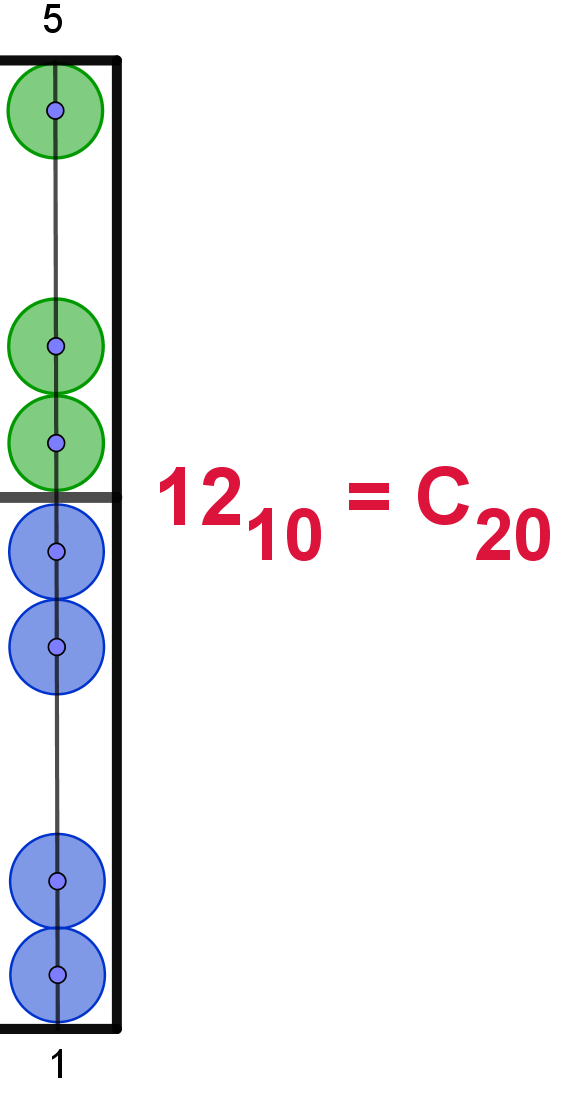
12 |
C |
|
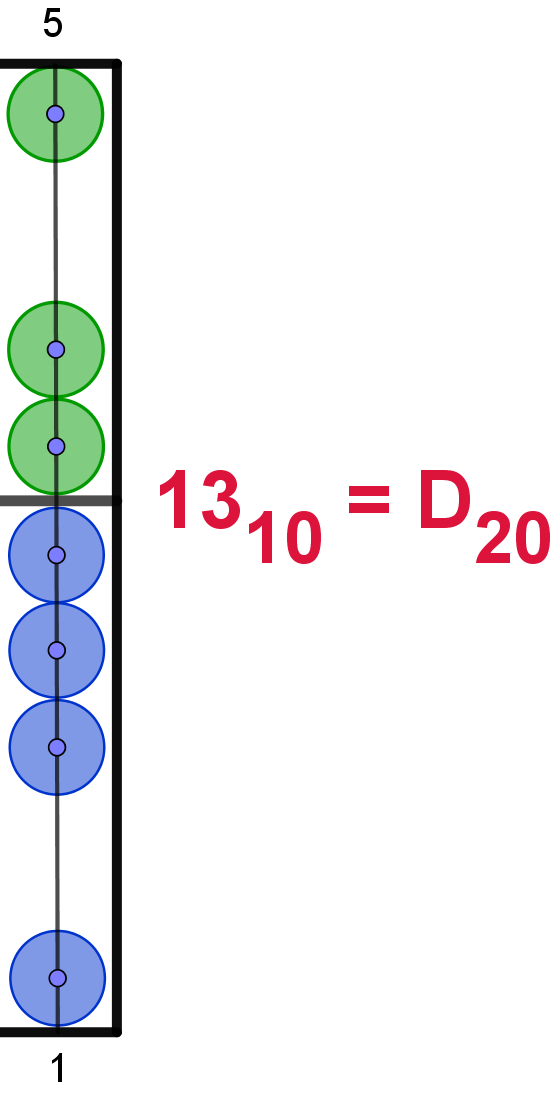
13 |
D |
|
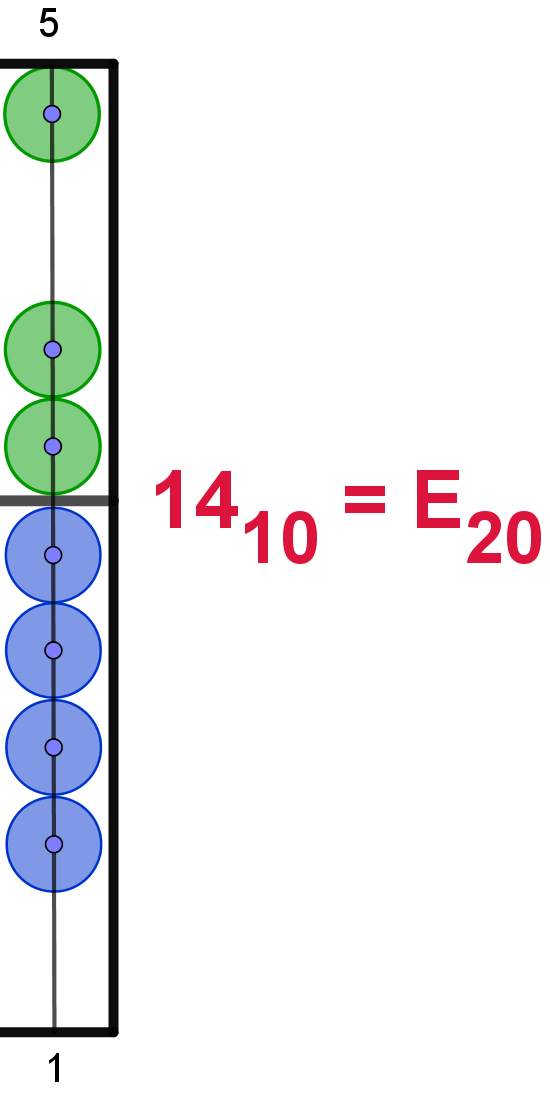
14 |
E |
|
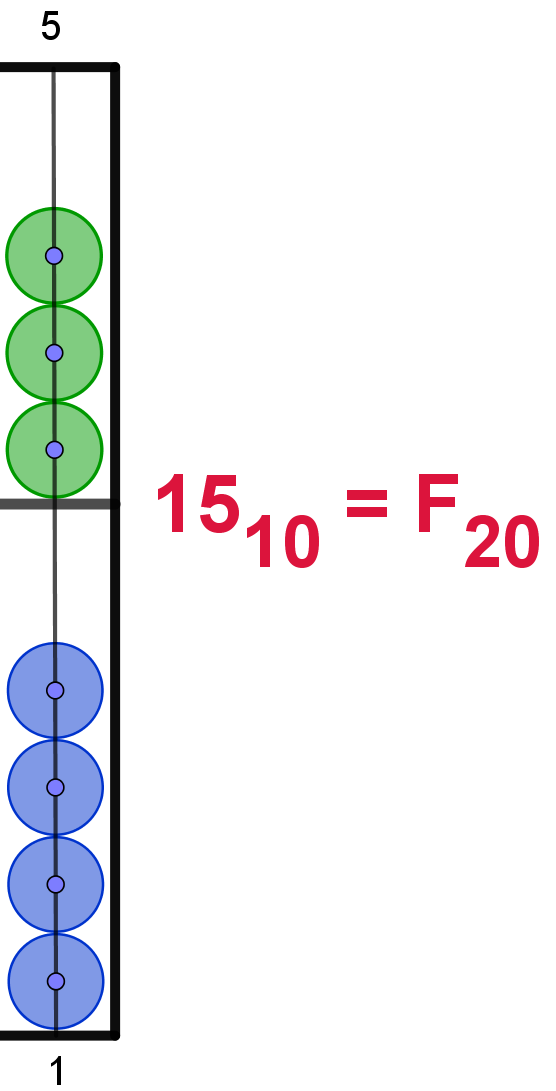
15 |
F |
|
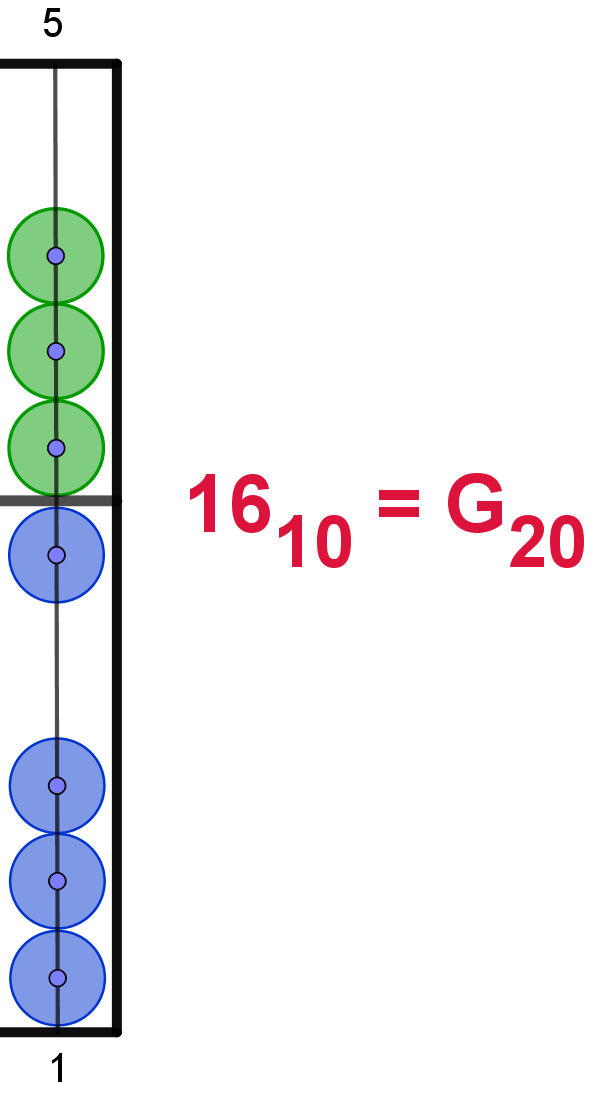
16 |
G |
|
17 |
H |
|
18 |
J |
|
19 |
K |
|
20 |
10 |
So werden die Zahlen von 110 bis 2010
im 20er-Zahlsystem, sowie weitere exemplarische Zahlen, auf dem maya Abakus
dargestellt.
zurück zum Seitenanfang
Wie man mit einem maya Abakus rechnet
Hier die Beispielaufgabe für das
"einfache" Rechnen:
im Dezimalsystem soll unsere Aufgabe lauten:
129110 + 88710 = ?
im 20er-Zahlsystem lautet die Aufgabe so (in
Anlehnung an das Hexadezimalsystem bekommt 1110 das B20
zugeordnet):
34B20 +
24720 = ?
|
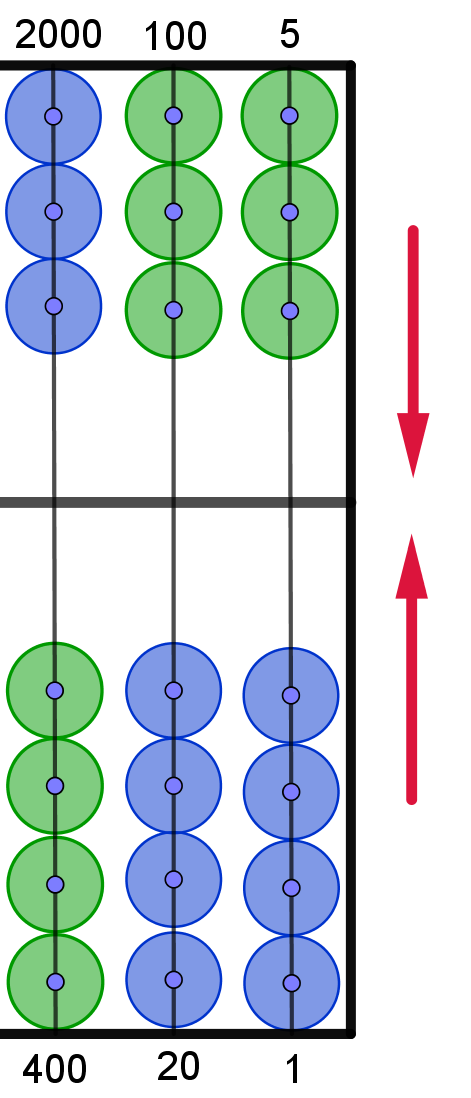
1. Lösungsschritt:
|
Bei der Grundstellung
liegen alle Perlen
oben bzw. unten am Rahmen.
|
|
|
|
|
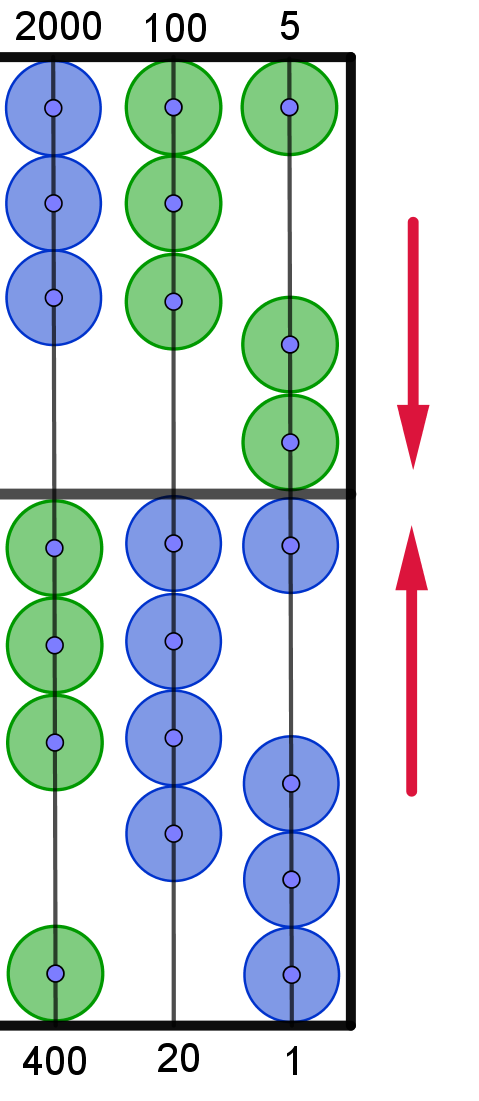
2. Lösungsschritt:
|
Zuerst schiebt man die
34B20
auf den Rahmen, d.h.:
3 Perlen in der 3. unteren Spalte,
4 Perlen in der 2. unteren Spalte und
1 Perle in der 1. unteren Spalte sowie 2 Perlen
in der 1. oberen Spalte
|
|
|
|
|
3. Lösungsschritt:
|
Jetzt addiert man,
ausgehend von der 3. Spalte, durch
Schieben schrittweise die 24720
dazu, also
zuerst plus 2.
|
|
3.1. Lösungsschritt:
|
Man verschiebt zuerst 1 Perle der 3.
unteren Spalte nach oben.
|
|
|
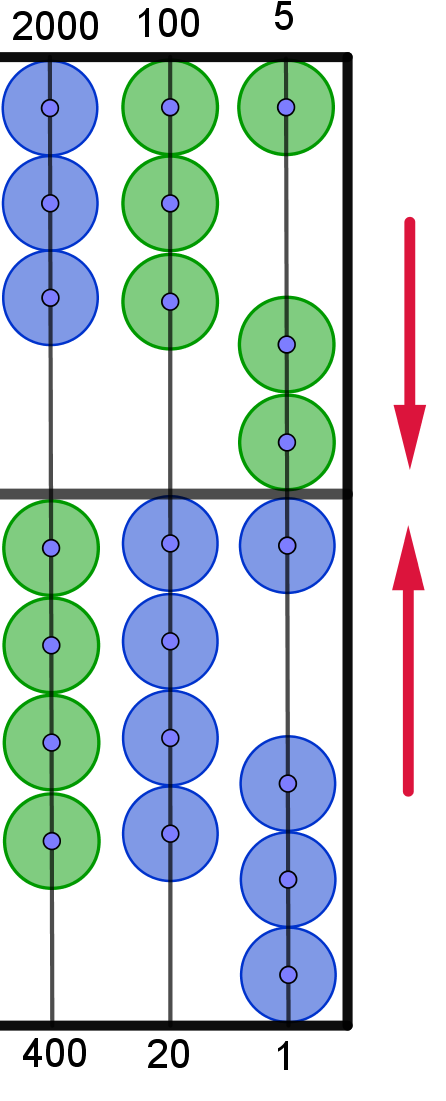 |
|
3.2. Lösungsschritt:
|
Nun verschiebt
man 1 weitere Perle der 3. unteren Spalte nach oben. Das geht
natürlich nicht.
D.h. nun muss
man eine neue Bündelung
vornehmen. 1 Perle der oberen 3. Spalte wird nach unten verschoben. Und,
die 4 Perlen der unteren Spalte werden nach unten verschoben.
|
|
|
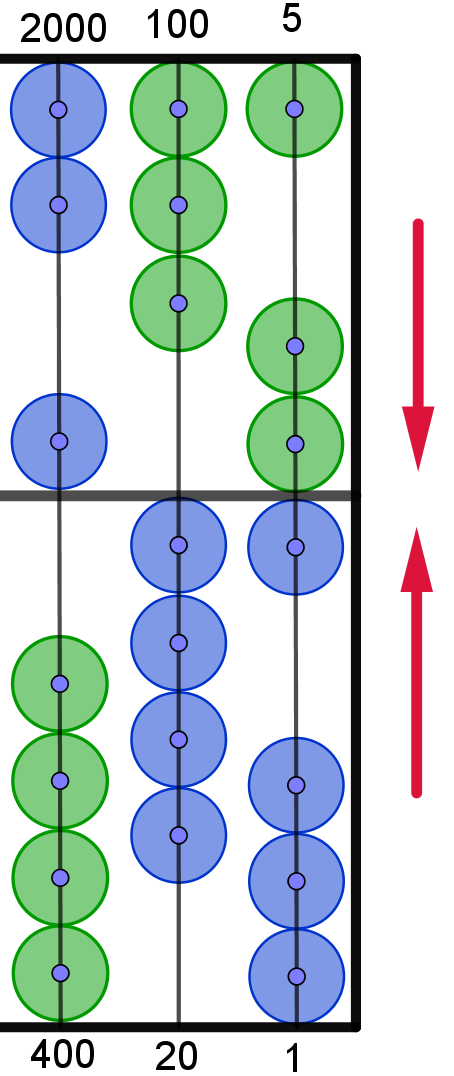
|
|
4. Lösungsschritt:
|
Jetzt addiert man
in der 2. Spalte die 4.
|
|
4.1. Lösungsschritt:
|
Dazu verschiebt man erst einmal 1 Perle
der 2. unteren Spalte nach oben. Das geht natürlich nicht.
D.h. nun muss man eine neue Bündelung
vornehmen. 1 Perle der oberen 2. Spalte wird nach unten verschoben. Und,
die 4 Perlen der unteren 2. Spalte werden nach unten verschoben.
|
|
|
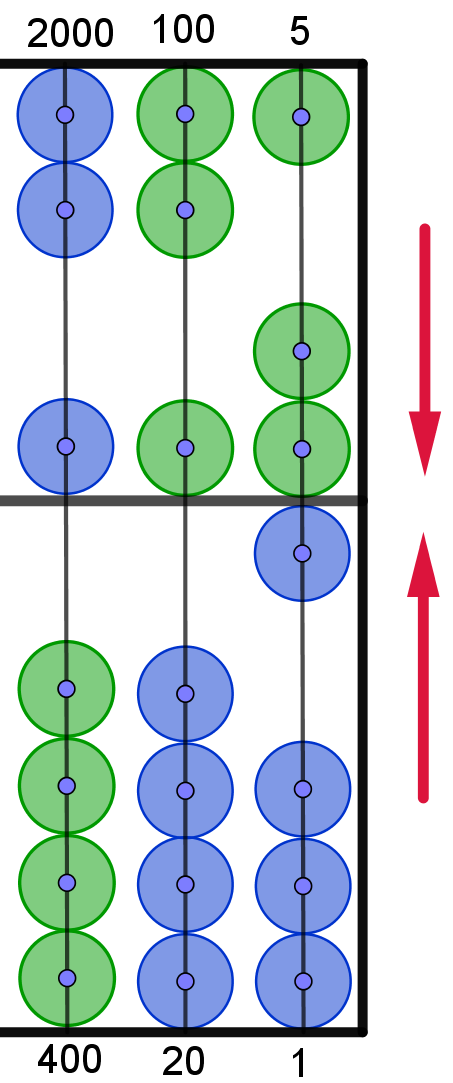
|
|
4.2. Lösungsschritt:
|
Nun verschiebt man 3 weitere Perlen der
2. unteren Spalte nach oben. |
|
|
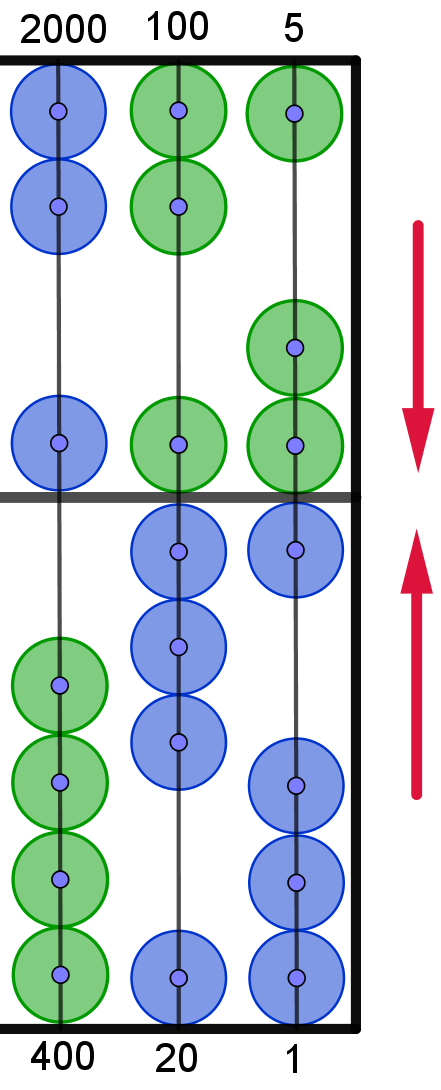 |
|
5. Lösungsschritt:
|
Jetzt addiert man in der 1. Spalte die
Zahl 7. |
|
5.1. Lösungsschritt:
|
Dazu verschiebt man erst
einmal 3 Perlen der 1. unteren Spalte nach oben. |
|
|
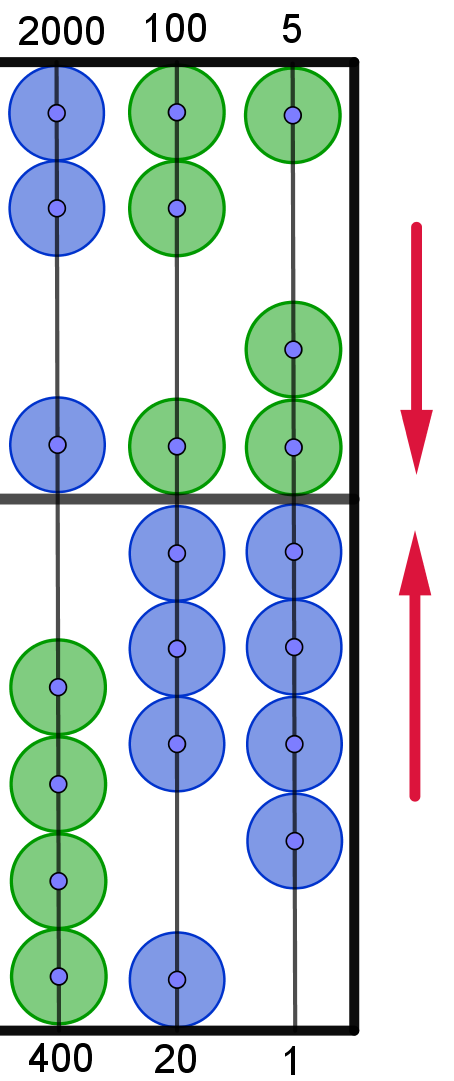 |
|
5.2. Lösungsschritt:
|
Nun verschiebt
man erst einmal 1 (von den verbleibenden 4 Perlen) weitere Perle der
1. unteren Spalte nach oben. Das geht natürlich nicht.
D.h. nun muss
man eine neue Bündelung
vornehmen. Eine weitere Perle der oberen 1. Spalte wird nach unten
verschoben. Und, die 4 Perlen der unteren Spalte werden nach unten
verschoben.
|
|
|
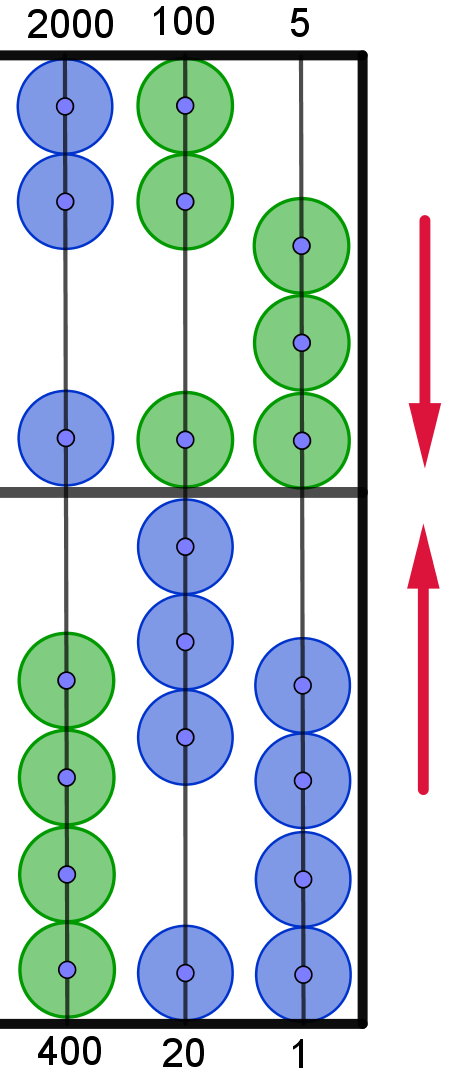
|
|
5.3. Lösungsschritt:
|
|
|
|
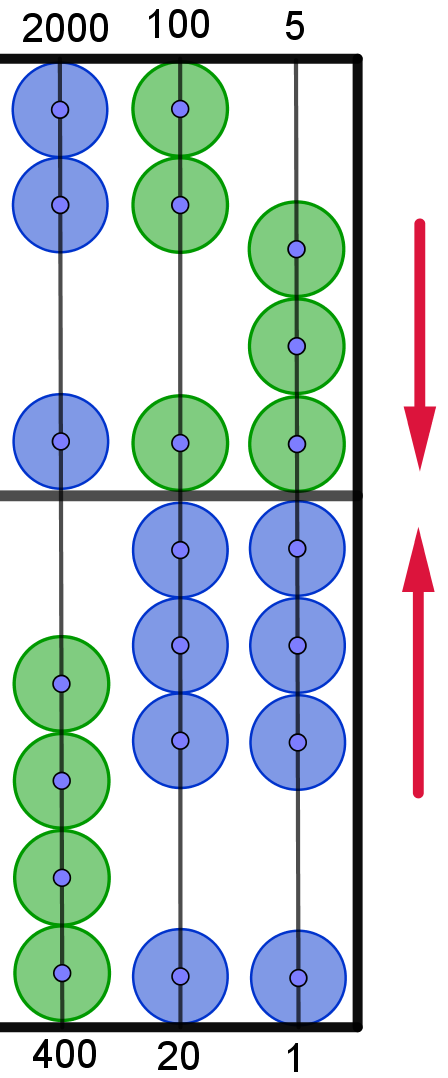 |
|
|
FERTIG
|
|
6. Lösungsschritt:
|
Jetzt kann das
Ergebnis abgelesen werden:
1 Perle in der 3. Spalte oben bedeutet 5,
1 Perle in der 2. Spalte oben und 3 Perlen in der 2.
Spalte unten bedeutet 8,
3 Perlen in der 1. Spalte oben und 3 Perlen in der 1.
Spalte unten bedeutet J,
Die Lösung lautet folglich:
58J20
|
|
|
|
|
|
34B20 +
24720
= 58J20 |
zurück zum Seitenanfang